Frontiera della massima disuguaglianza
Definizione
La Frontiera della Massima Diseguaglianza o, più elegantemente e in lingua originale, Inequality Possibility Frontier (d’ora in avanti IPF) è un concetto che mette in relazione il grado di sviluppo di una economia, rappresentato dal reddito medio pro-capite espresso in termini di salario di sussistenza, e il massimo indice di Gini raggiungibile. Tale concetto è stato introdotto per la prima volta in letteratura dall’articolo “Pre-Industrial Inequality” di Milanovic et al. (2011) ed è stato poi perfezionato dallo stesso Milanovic in uno studio successivo (2013).
L’idea alla base di questa misura è abbastanza semplice: si supponga che in una società (in qualsiasi tempo e spazio) si debba distribuire il reddito prodotto in misura tale che almeno tutte le persone ricevano un reddito pari a quello di sussistenza, il rimanente è il surplus che può essere estratto dalla classe dominante e che, quindi, genera diseguaglianza. Nel caso non si distribuisse alla classe più povera almeno il reddito di sussistenza, si assisterebbe alla morte delle persone al di sotto del minimo di sussistenza o, più probabilmente, a una loro rivolta che modificherebbe l’assetto istituzionale vigente. Il reddito di cui si può appropriare la classe dominante è quindi dipendente dal reddito complessivo della società. Indicando con s il salario minimo di sussistenza e con μ il reddito medio, se s = μ la diseguaglianza risulta nulla e l’indice di Gini pari a zero. Tuttavia, al crescere del reddito prodotto dalla società, il reddito medio cresce e si allontana da s. In questo modo, il surplus che le classi ricche possono estrarre aumenta (esso è pari a [(μ - s) * N], cioè alla differenza tra il reddito medio e il salario minimo di sussistenza, moltiplicata per la popolazione totale). Conseguentemente, aumenta anche la diseguaglianza che caratterizza la società.
Per fare un esempio, ipotizzando una società composta da 100 persone, di cui una sola fa parte della classe ricca, il salario minimo di sussistenza è pari a 10 unità e il reddito totale prodotto da questa società è 1050 unità (il reddito medio è quindi μ = 1050/100 = 10,5). Tutti e 99 i membri della classe povera ricevono un reddito di dieci unità, per un aggregato di 990, mentre l’unico membro della classe ricca riceve 60 unità di reddito. La diseguaglianza in questa società, misurata dall’indice di Gini, è quindi pari a G = 0,047. Se, in un momento successivo, il reddito totale prodotto passa a 2000 unità, e la somma che va alla classe povera è sempre costante e uguale a 990, il reddito dell’unico individuo della classe ricca è pari a 1010, con un indice di Gini che cresce fino ad arrivare al valore di G = 0,495. Come detto, la IPF è utile perché consente di determinare la massima diseguaglianza raggiungibile da una società date alcune variabili base: s (il salario minimo di sussistenza), μ (il reddito medio dell’intera popolazione), N (il numero di persone nell’intera società) ed ε (la quota, molto piccola, di persone appartenenti alla classe ricca).
Formalizzazione
È possibile ora definire la IPF in termini più formali: il reddito medio ricevuto dai membri della classe ricca è yh = (μN - sN(1-ε))/εN che equivale a yh = 1/ε [μ - s(1 - ε)]. Calcolando i valori che può assumere l’indice di Gini al crescere di μ, si trova il locus dell’indice stesso, ovvero la frontiera del massimo valore che l’indice può assumere per ogni dato valore di μ e s. È possibile ora rappresentare graficamente i risultati ottenuti in un grafico cartesiano, dove sull’asse delle ordinate si è disegnato il valore massimo dell’indice di Gini mentre sull’asse delle ascisse è rappresentato il reddito medio in rapporto al reddito di sussistenza (Figura 1).
Figura 1. Inequality Possibility Frontier
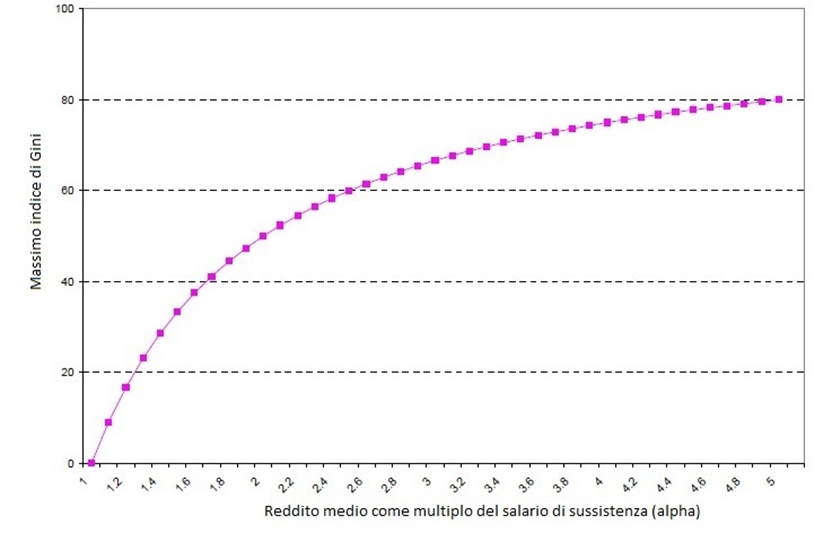
Ipotizzando che ogni membro nelle due classi (poveri e ricchi) riceva un reddito pari a quello medio della classe, cioè s per i poveri e yh per i ricchi, è possibile calcolare l’indice di Gini utilizzando la formula che segue:
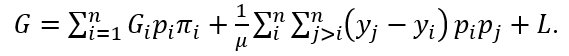
Il termine L è il termine di overlap, che viene per ora considerato nullo in quanto, per ipotesi, ogni individuo riceve il reddito medio della classe di appartenenza. Il primo termine della somma è la componente within (anch’essa nulla se all’interno delle classi gli individui ricevono lo stesso reddito) mentre il secondo riflette la diseguaglianza between (dovuta alla differenza tra le due classi). I termini pi e πi sono, rispettivamente, la proporzione di persone e la proporzione di reddito sul totale della popolazione considerata, mentre Gi è la diseguaglianza interna alla classe i. Sostituendo al posto di L e Gi zero, ed effettuando le semplificazioni per considerare le sole due classi, si ottiene:
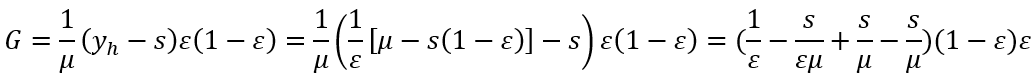
che equivale a G = (1 - ε)(μ - s)/μ. Se ora si scrive il reddito medio in termini di reddito minimo di sussistenza (cioè come multiplo di esso), si ottiene μ = αs, dove α ≥ 1, e si può riscrivere la formula per il calcolo dell’indice di Gini come: G = (1 - ε)(αs - s)/αs = (1 - ε)(α - 1)/α. L’indice di Gini dipende quindi dalla quota di individui ε che rappresentano la classe ricca e dal parametro α che è il rapporto tra il reddito medio e il reddito minimo di sussistenza.
Estensioni
Da questa versione semplificata è possibile derivare altre forme della IPF, che tengano conto anche di altri fattori. Ad esempio, Milanovic (2013) introduce l’elasticità del salario minimo al reddito medio, tale per cui un aumento del reddito medio causa un aumento del salario minimo. Il reddito che deve essere distribuito ai membri della classe povera non è più, quindi, quello di sussistenza, ma viene definito ‘sociale’ perché il suo livello dipende dinamicamente dalla società presa in esame.
La IPF risulta quindi molto utile per poter stabilire il livello massimo che può raggiungere l’indice di Gini in una data società, in particolare se si considerano paesi con un reddito medio molto basso – come alcuni dei paesi attualmente in via di sviluppo o molte società di epoche preindustriali.
Riferimenti bibliografici
- Milanovic B., P.H. Lindert e J.G. Williamson (2011), “Pre‐Industrial Inequality”, The Economic Journal, 121(551), 255–272. Link
- Milanovic B. (2013), “The inequality possibility frontier: extensions and new applications”, World Bank Working Paper Series, 6449.
Suggerimenti di lettura
- Alfani G. e W. Ryckbosch (2016), “Growing apart in early modern Europe? A comparison of inequality trends in Italy and the Low Countries, 1500–1800”, Explorations in Economic History, 62(C), 143-153.
- Malanima P. (2018), “Italy in the Renaissance: a leading economy in the European context, 1350–1550”, The Economic History Review, 71, 3-30.


